Cet article s’adresse à un public ayant des connaissances de modélisation (régression logistique) et du langage R, souhaitant s’initier au Deep Learning par une approche pratique. Mon objectif est de partager ma compréhension avec vous, toujours en l’appuyant avec des éléments concrets: du code et des graphiques.
Deep Learning est sans doute un des gros buzzwords de ces dernières années. Dans ce qui suit, on ne s’attardera pas sur le côté théorique de la question, celui-ci méritant plus qu’un petit article comme celui-ci & ayant été largement traité par des experts (lien).
Dans l’esprit learning by doing, adoptons plutôt une approche très pratique des choses. Dans ce qui suit, nous allons à partir de rien et en allant droit au but construire un réseau de neurones simple.
L’objectif est de déconstruire et fragmenter ce fameux réseau de neurones pour le démystifier et en éliminer la complexité.
Nous utiliserons la célèbre régression logistique comme réference pour expliquer en quoi un réseau de neurones est différent.
Après tout, les briques de base du réseau de neurones n’ont rien de compliqué, mais les chercheurs & ingénieurs rivalisent de créativité pour en agencer des centaines voir des milliers dans des architectures ayant des fonctions avancées. Ainsi aujourd’hui grâce au Deep Learning :
- On fait de la reconnaissance d’images (essayez ici),
- On traduit du texte,
- On prédit des évolutions de prix,
- On fait courir knacki man
- On bat des champions du monde du jeu de Go !
Dans ce qui suit, je m’efforce de progresser de manière claire et concrète, appuyée & illustrée par du code clair en R.
Parce qu’une image vaut mieux qu’un long discours, nous mettrons l’accent sur la visualisation.
I. Notre baseline : la régression linéaire
On se place dans le plan: imaginons 250 balles de couleurs bleu & rouge disposées sur une table, caractérisées par leurs coordonnées dans le plan : x et y. La couleur de la balle (class) est la variable à expliquer, les coordonnées x et y en sont les prédicteurs ou variables explicatives. Notre tâche consistera à créer un modèle capable d’apprendre une frontière de séparation entre les classes à partir des coordonnées des points.
1. Avec des données simples
Commençons par créer des données dans une configuration simple. Deux “tas”, bien séparés. Je génère un jeu de données appelé biclust grâce à la fonction rnorm() de R qui prend en argument un nombre de points (nb) ainsi que les paramètres de la distribution sous laquelle on les génère (la moyenne (mean) et l’écart type (sd) de la Loi Normale) :
nb = 125 ; sd = 1.5
biclust <- rbind(data.frame(x1 = rnorm(nb, mean = 2,sd),
x2 = rnorm(nb, mean = 2.5,sd),
class = rep('Rouge',nb)),
data.frame(x1 = rnorm(nb, mean = 7.5,sd),
x2 = rnorm(nb, mean = 7.5,sd),
class = rep('Bleu',nb)))Les données ressemblent à ça :
## x1 x2 class
## 1 3.160324 0.5948671 Rouge
## 2 1.260425 3.9362716 Rouge
## 3 2.069410 3.1488253 Rouge
## 4 3.014580 3.0889915 Rouge
## 5 1.093936 2.6676533 Rouge
## 6 1.394444 2.6336675 RougeEt un petit graph ggplot2 (je ne mettrais pas le code par la suite, pour simplifier) :
theme_set(theme_minimal())
ggplot(biclust) +
aes(x1, x2, colour = class) +
geom_point() +
labs(x = 'x1',y = 'x2')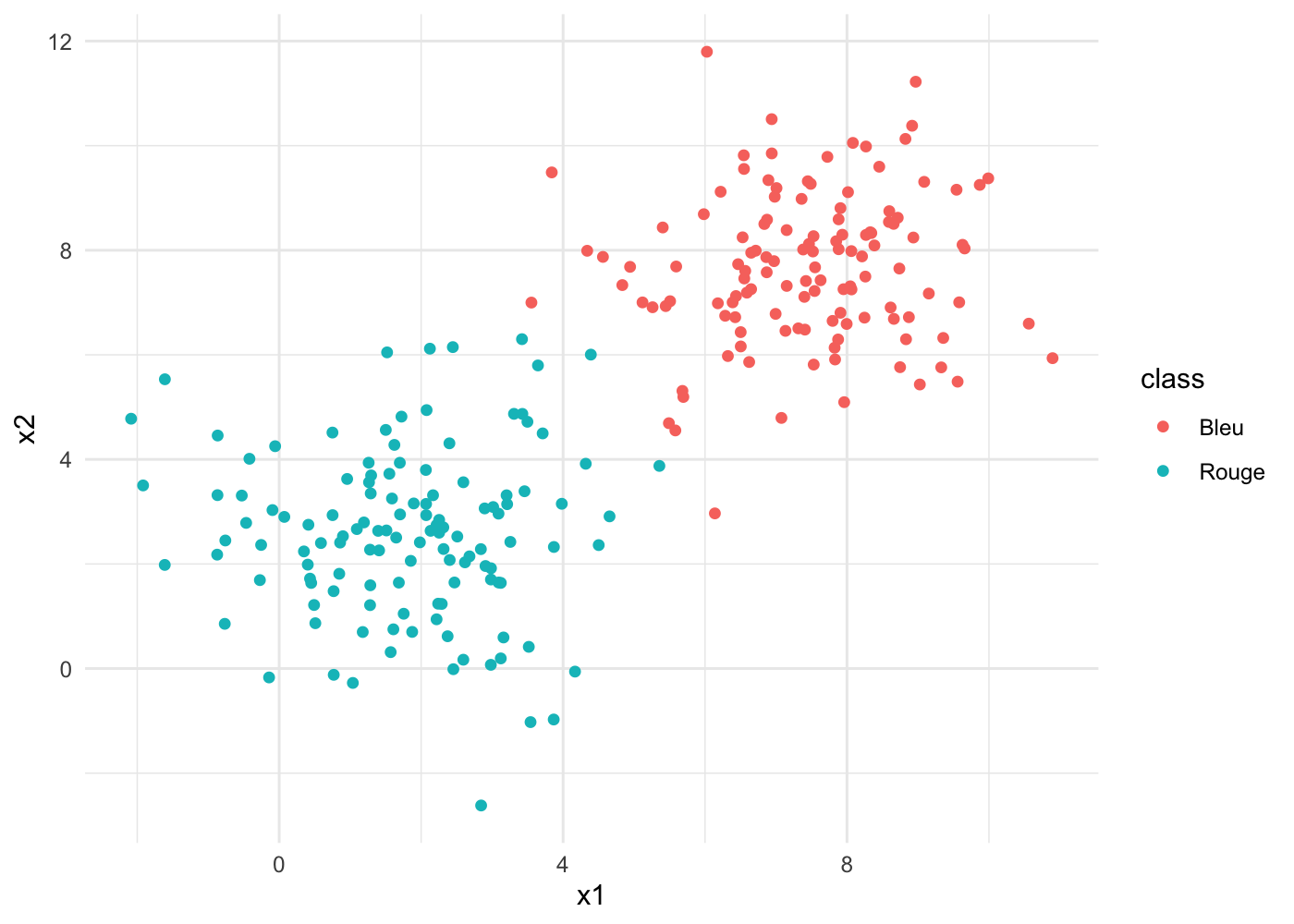
Comment séparer automatiquement les points rouges des bleus ? On remarque que : a. Nous sommes face à un problème de classification binaire (deux classes à séparer), b. Les points ne sont pas mélangés, il est donc possible de les séparer facilement avec une droite. Une fonction affine bien placée devrait faire l’affaire,
L’intuition ici est d’employer un modèle linéaire. Essayons avec un modèle logistique, la solution classique dès qu’il s’agit de classification binaire :
logreg <- glm(as.factor(class) ~ x1 + x2, family = binomial, data = biclust)Voici la manière dont notre modèle performe, que l’on peut voir à la qualité de séparation entre points bleus et rouges :
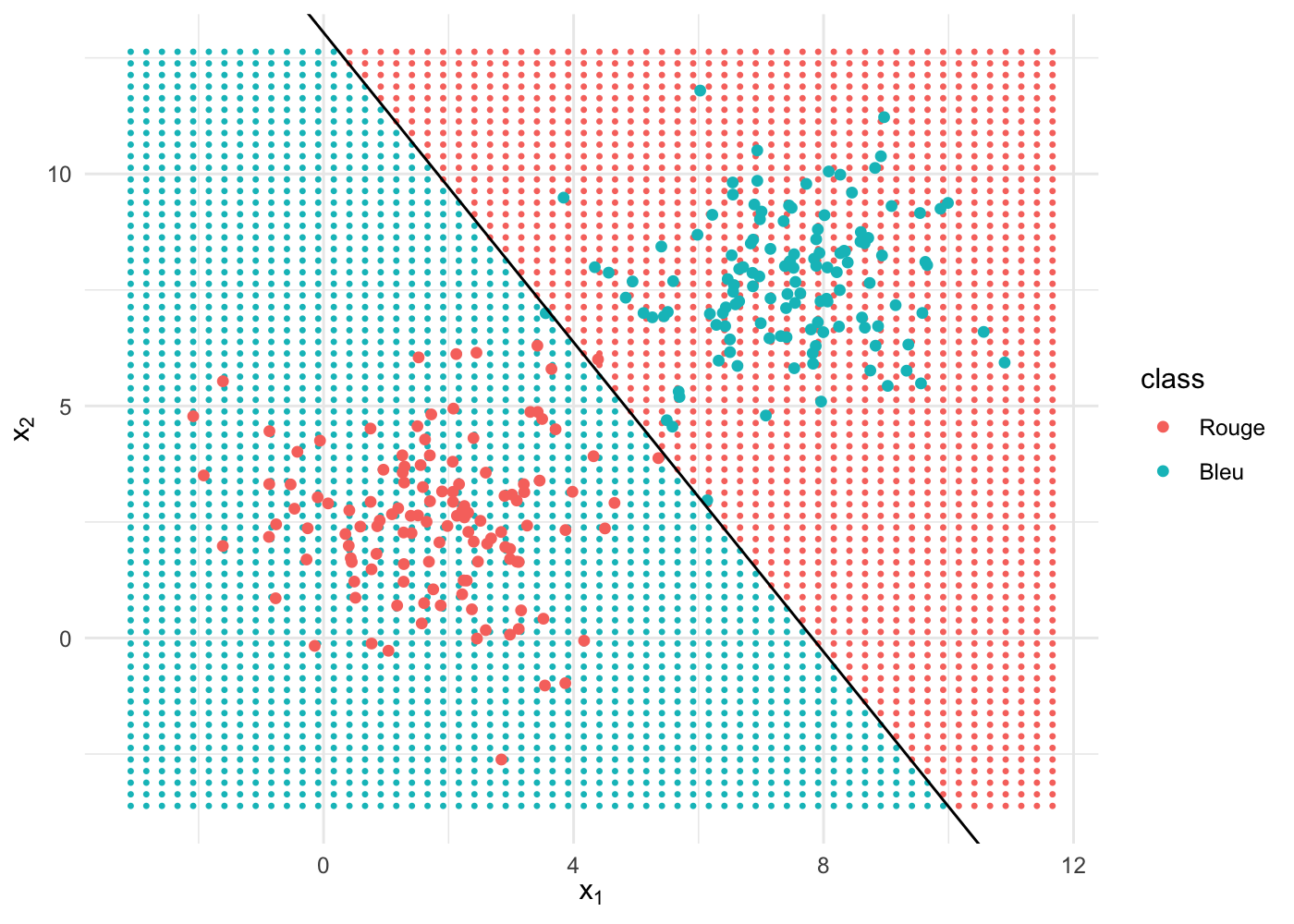
La séparation, représentée par une frontière linéaire, est quasi-parfaite. En effet, nous avons utilisé un algorithme d’apprentissage supervisé, le modèle linéaire (une droite de la forme ), pour résoudre un problème linéaire, c’est super, tout roule ! 👌
2. Essayons à présent avec des données plus “complexes” :
Commençons par fabriquer un ensemble de 250 balles avec une forme un peu plus exotique … la spirale, tiens ! 🌀
deux_spirales <- function(N = 250,
rad = 2*pi,
th0 = pi/2,
labels = 0:1) {
N1 <- floor(N / 2)
N2 <- N - N1
theta <- th0 + runif(N1) * rad
spiral1 <- cbind(-theta * cos(theta) + runif(N1),
theta * sin(theta) + runif(N1))
spiral2 <- cbind(theta * cos(theta) + runif(N2),
-theta * sin(theta) + runif(N2))
points <- rbind(spiral1, spiral2)
classes <- c(rep(0, N1), rep(1, N2))
data.frame(x1 = points[, 1],
x2 = points[, 2],
class = factor(classes, labels = labels))
}
set.seed(42)
spiral <- deux_spirales(labels = c('Rouge', 'Bleu'))Graphiquement :
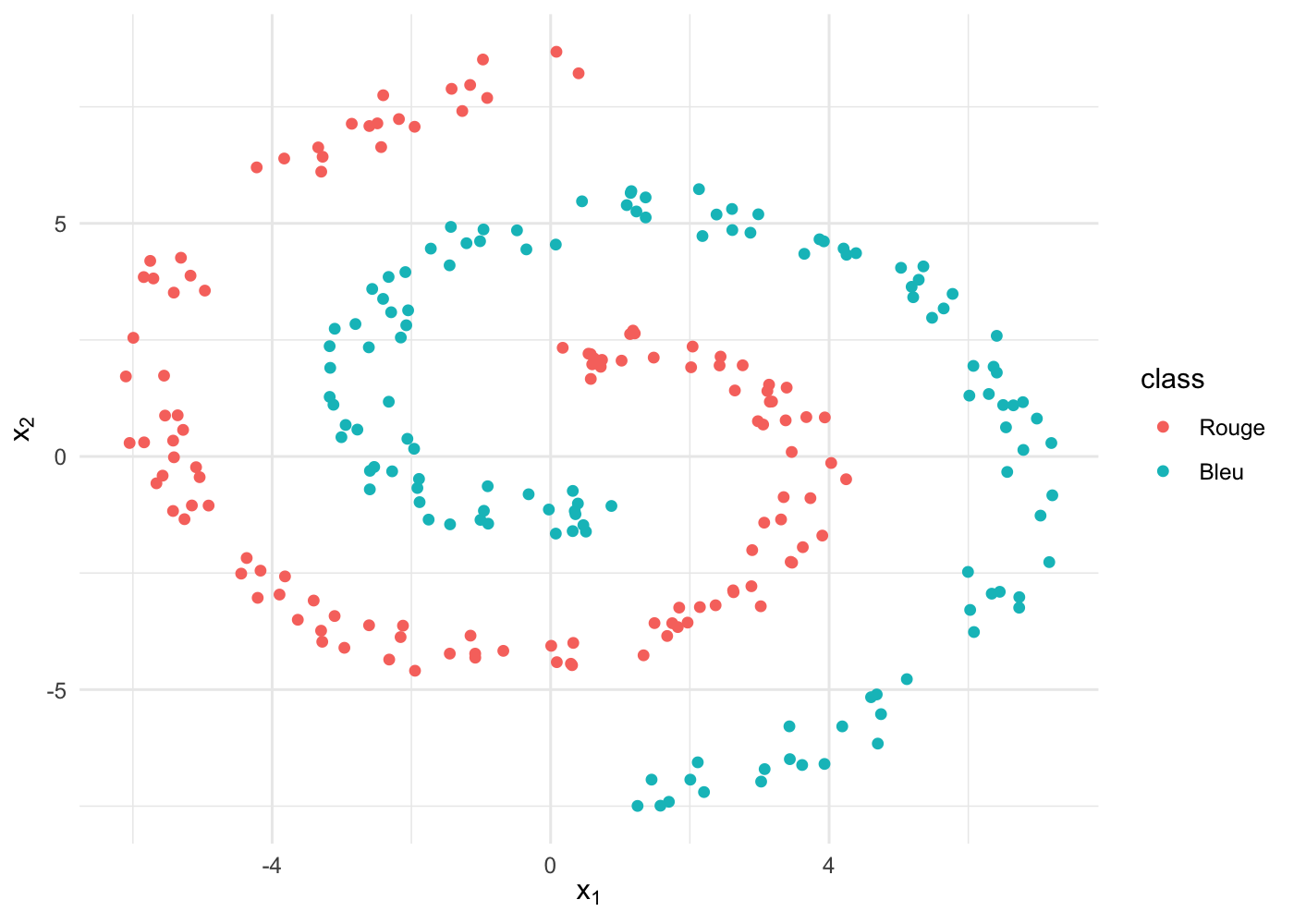
Commençons par tester ce qu’on sait déjà faire, la régression logistique :
logreg <- glm(class ~ x1 + x2, family = binomial, data = spiral)
correct <- sum((fitted(logreg) > .5) + 1 == as.integer(spiral$class))
print(correct/250*100)## [1] 56140 points sur 250 sont bien classifiés, soit une précision de 56 % seulement.
Visuellement, ça donne ça :
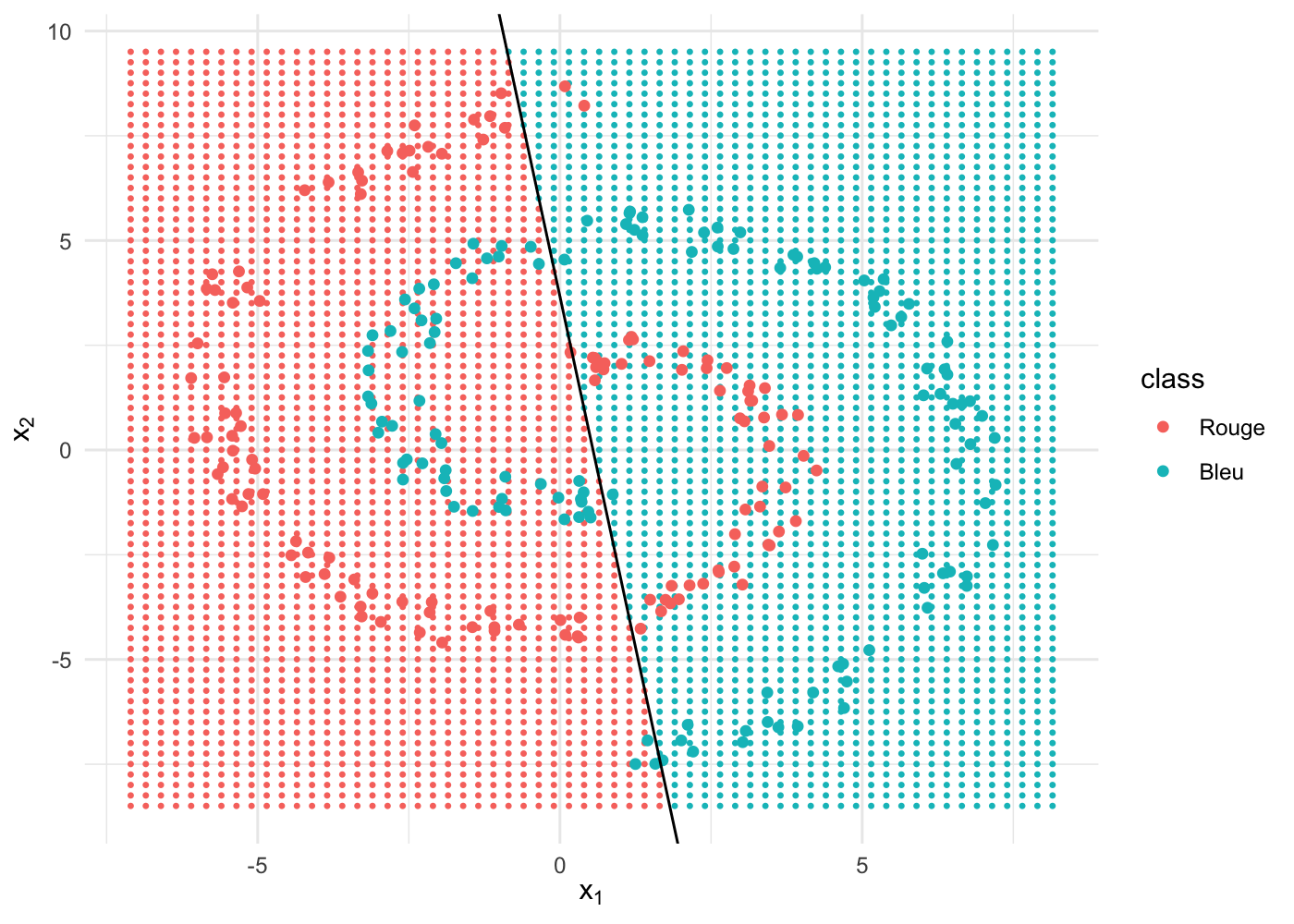
C’est pas top ! cette performance n’est pas acceptable.
II. Essayons de faire mieux, pourquoi pas avec un réseau de neurones artificiels ?!
1. Fonctionnement général et composants
Un réseau de neurone est un approximateur de fonction universel. C’est à dire qu’il va apprendre une représentation des données qu’on lui donne, y compris complexes, sous une forme approximée par un réseau de fonctions. La brique de base du réseau de neurones est le neurone (ou perceptron).
Comme vous l’avez deviné, les réseaux de neurones artificiels sont inspirés des neurones biologiques. La théorie derrière n’a rien de nouveau.
Un neurone est une unité de calcul. Elle prend plusieurs valeurs en entrée et renvoie une sortie calculée, comme ceci (source) :
Dans notre cas, les données en entrée x1 et x2 sont combinées dans une fonction linéaire du type , les W étant des coefficients donnant plus ou moins de poids à la variable selon son importance dans la sortie. Le résultat de cette fonction passe ensuite dans une fonction d’activation appelée Sigmoïde (ou fonction logisitique !) qui a plein de propriétés intéressantes dont celle de placer la sortie dans l’intervalle continu . Génial, une probabilité ! nous voulions justement prédire les chances d’un point d’être bleu plutôt que rouge (ou l’inverse, peu importe). Rappelons que lors de l’étude d’un phénomène donné, la somme des probabilité de réalisation des différentes possibilités est toujours égale à 1 .
La puissance du perceptron se révèle lorsqu’il travaille en réseau avec un grand nombre de ses copains, organisés en couches successives. L’architecture la plus fréquente, le perceptron multi-couches feed-forward dense (ou fully-connected car tous les neurones d’une couche sont connectés à tous ceux de la prochaine) se présente comme suit :

Source : analyticsvidhya.com
Les couches cachées sont celles qui n’interagissent pas avec l’extérieur. Elles sont internes au réseau.
2. A l’attaque, codons notre premier réseau de neurones !
Codons un réseau à une couche cachée. Comme pour tout modèle, une fois que l’on a défini ses propriétés (paramètres), vient la phase d’entraînement qui consiste à montrer les données au modèle afin qu’il apprenne dessus.
a. D’abord, l’architecture globale
Nous allons coder un réseau dans lequel les données progressent toujours en avant (feed-forward). l’information se déplace dans une seule direction, de la couche d’entrée à la couche de sortie en passant par les différentes couches cachées, dans l’ordre, comme dans le schéma précédent.
En termes de code, ça ressemble à ceci. On en profite pour faire en sorte que chaque neurone applique une sigmoïde (fonction logistique) juste avant de renvoyer sa sortie, on parle de fonction d’activation.
Nous allons écrire une fonction feedfwd() qui dans l’ordre :
* Prend en entrée les variables explicatives (x), et deux vecteurs de poids (w1 et w2)
* Multiplie x par w1 et lui applique la fonction d’activation
* Le résultat de l’étape précédente subit la même opération avec le vecteur w2, puis est retourné. La sortie est un vecteur de probabilités.
# La fonction logistique
sig <- function(x) 1 / (1 + exp(-x))
# L'opérateur %*% sert à la multiplication de matrices
feedfwd <- function(x, w1, w2) {
z1 <- cbind(1, x) %*% w1
h <- sig(z1)
z2 <- cbind(1, h) %*% w2
list(output = sig(z2), h = h)
}b. Ensuite, rajoutons un peu d’intelligence avec la rétro-propagation du gradient
La rétro-propagation du gradient est le cœur de la machinerie permettant d’entraîner un réseau de neurones. C’est elle qui permet progressivement de trouver les poids optimaux qui font que notre modèle est “bon”. La rétro-propagation permet au modèle d’apprendre de ses erreurs de manière itérative et de s’améliorer au fur et à mesure qu’il ingère les données. Les poids qui contribuent à engendrer une erreur importante se verront modifiés de manière plus significative que les poids qui ont engendré une erreur marginale, dans la direction de la minimisation de l’erreur globale du réseau. L’algorithme du gradient a pour but de converger de manière itérative vers une configuration optimale des poids, permettant le meilleur ajustement de modèle possible.
Quelques points à ce sujet :
- Tout algorithme d’apprentissage supervisé a pour objectif d’apprendre une structure de données à partir d’une base d’apprentissage. Pour ce faire, il a besoin de trouver la combinaison de poids qui permet la meilleure approximation des données d’apprentissage.
- Pour atteindre ce meilleur ajustement, on optimise (= minimise la valeur) d’une fonction de coût (Objectif/Loss/Cost). Cette fonction de coût mesure l’écart entre les vrais données et les prédictions du modèle , c’est à dire l’erreur. Nous sommes bien face à un problème d’optimisation avec une fonction de coût à minimiser.
- Ce problème d’optimisation, en apparence complexe, se résout en fait assez efficacement grâce à l’algorithme de la descente du gradient. Le gradient est une généralisation de la notion de dérivée, dans le cas à plusieurs variables (vous trouverez ici une explication imagée et intuitive de l’algo). Dans l’espace à deux dimensions (2 variables), voici une illustration de l’algorithme (source) :
- On a ici deux coefficients de régression m et b à chercher de manière à ce que notre droite apprenne les données (encart de droite).
- Pour ce faire, on cherche le minimum de Error (encart de gauche) :
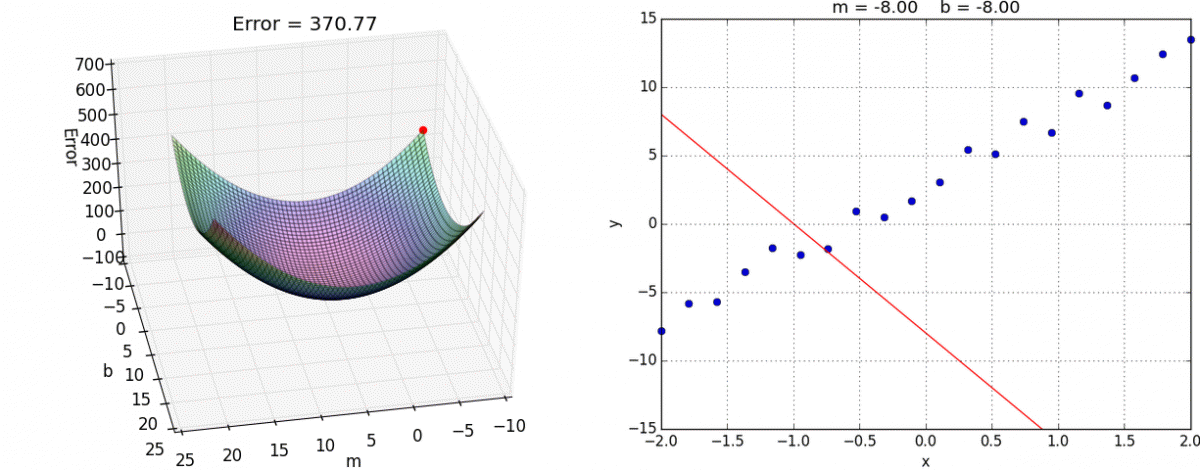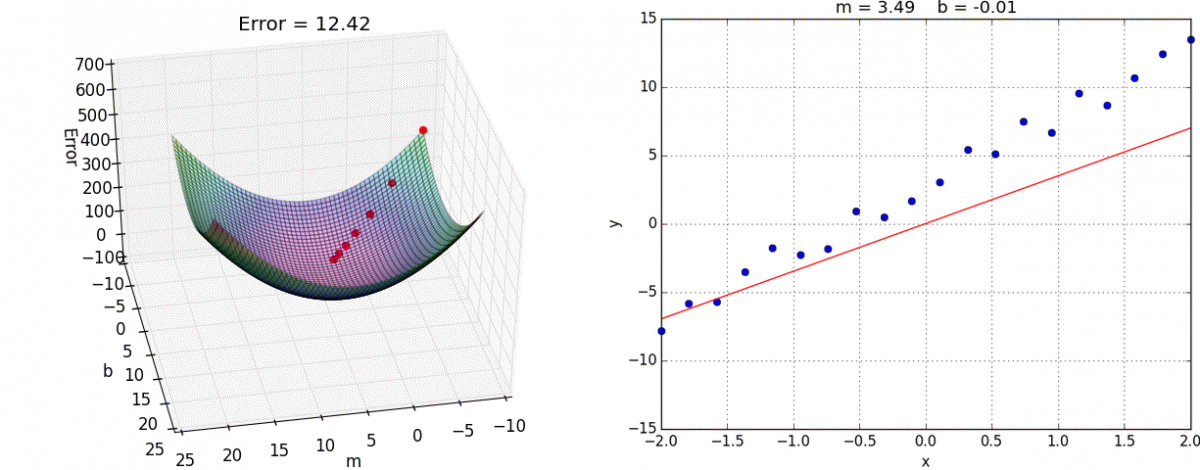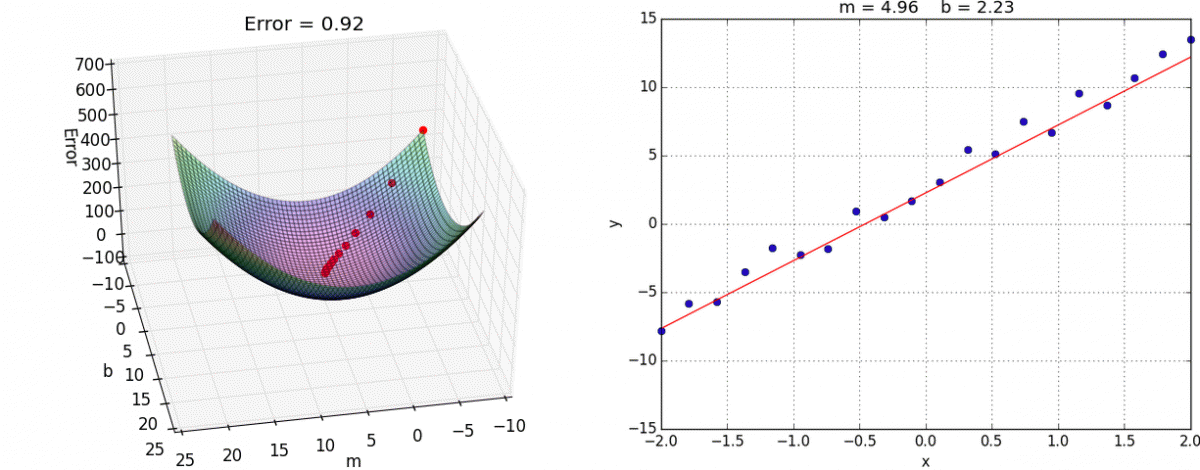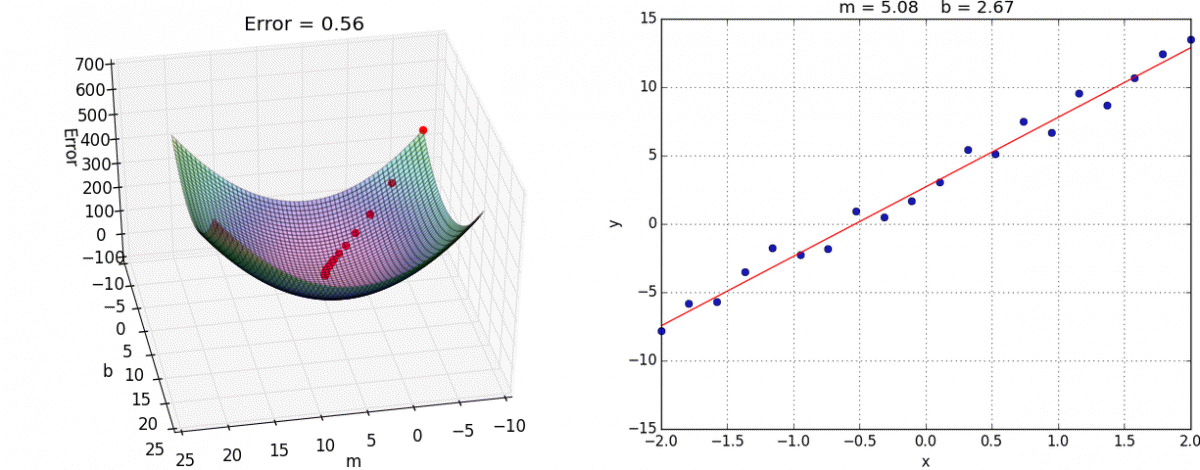
Hop :
backprop <- function(x, y, y_hat, w1, w2, h, learn_rate) {
dw2 <- t(cbind(1, h)) %*% (y_hat - y)
dh <- (y_hat - y) %*% t(w2[-1, , drop = FALSE])
dw1 <- t(cbind(1, x)) %*% (h * (1 - h) * dh)
w1 <- w1 - learn_rate * dw1
w2 <- w2 - learn_rate * dw2
list(w1 = w1, w2 = w2)
}c. Rassemblons tout ça et testons !
On définit donc une fonction train() permettant d’entraîner notre réseau de neurones, avec une architecture feed-forward et utilisant la rétro-propagation pour trouver les meilleurs paramètres. Les paramètres sont :
x: matrice comprenant les données d’apprentissage (les variablesx1etx2)y: vecteur contenant la variable réponse (label : “Rouge” ou “Bleu”)hidden: nombre de nœuds cachés de la couche cachéelearn_rate: learning rate ou taux d’apprentissage. Ce paramètre contrôle le pas avec lequel s’effectue la descente du gradient. Plus il est grand, et plus la descente se fait à grands pas et donc rapidement (en théorie), mais on prend le risque de “sauter” le minimum de la fonction. Prenons donc une petite valeur (par défaut 0.01)iterations: nombre d’itérations (une itération correspond à un passage des données dans le réseau suivi d’une mise à jour des coefficients par rétro-propagation)
Les poids w sont initialisés avec des valeurs aléatoires, donc pas besoin de les fournir à la fonction train() et on ré-utilise la fonction feedfwd() créée précédemment
train <- function(x, y, hidden = 5, learn_rate = 1e-2, iterations = 1e4) {
d <- ncol(x) + 1
w1 <- matrix(rnorm(d * hidden), d, hidden)
w2 <- as.matrix(rnorm(hidden + 1))
for (i in 1:iterations) {
ff <- feedfwd(x, w1, w2)
bp <- backprop(x, y,
y_hat = ff$output,
w1, w2,
h = ff$h,
learn_rate = learn_rate)
w1 <- bp$w1; w2 <- bp$w2
}
list(output = ff$output, w1 = w1, w2 = w2)
}Essayons avec le jeu de données en spirales avec une couche cachée composée de 5 nœuds et en faisant 100 000 itérations :
x <- data.matrix(spiral[, c('x1', 'x2')])
y <- spiral$class == 'Bleu'
nnet5 <- train(x, y, hidden = 5, iterations = 1e5)En termes de performance de prédiction, on est à 98 %, ce qui est vraiment pas mal avec des données complexes à saisir et un entrainement très rapide (10s sur un processeur M1)
Graphiquement, il est intéressant d’observer la forme de la frontière de décision, non linéaire mais assez anguleuse quand même. On commence à percevoir la puissance d’apprentissage des réseaux de neurones :
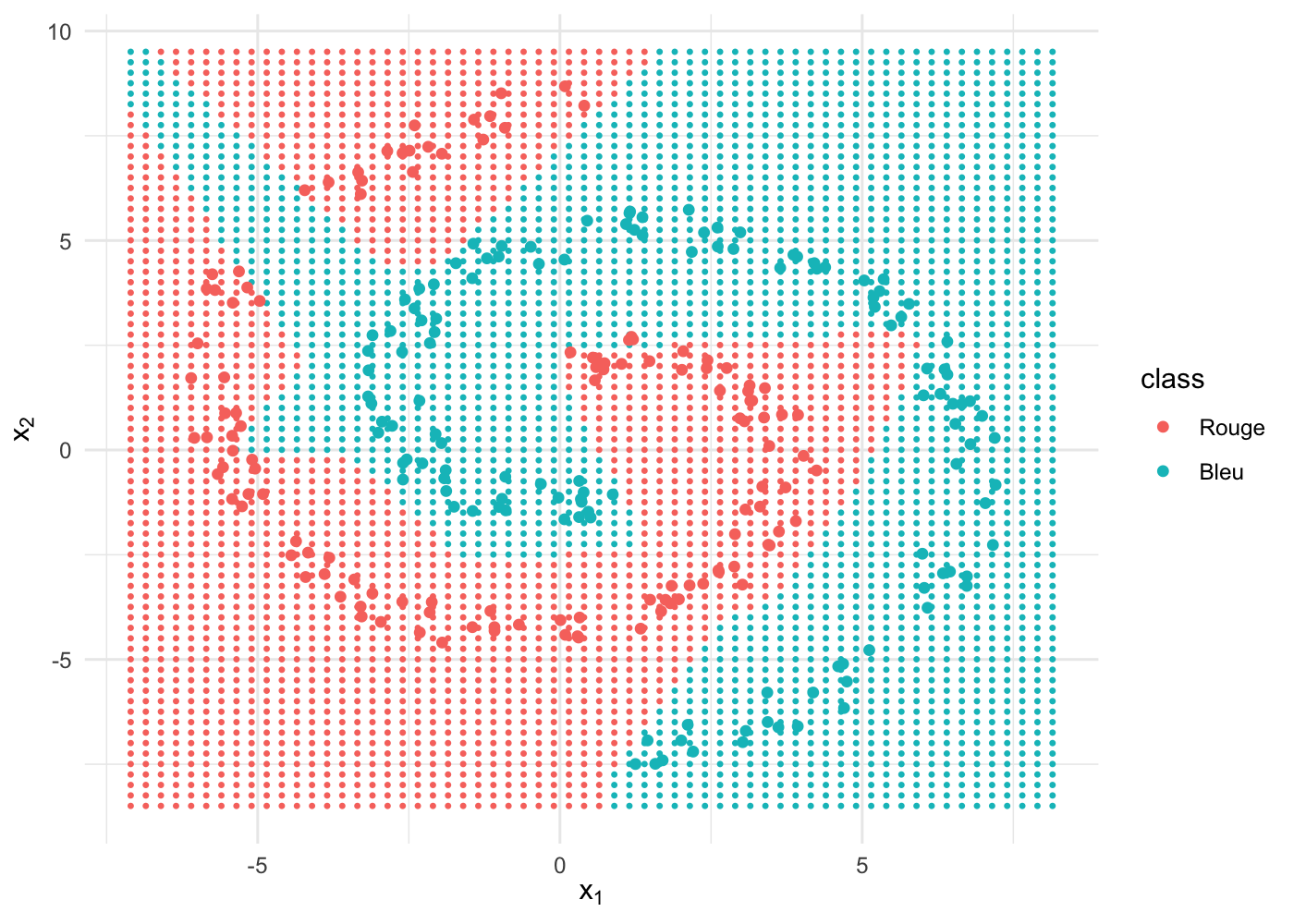
On entraîne à présent un réseau avec une couche cachée plus grande, constituée de 30 nœuds :
nnet30 <- train(x, y, hidden = 30, iterations = 1e5)
ff_grid <- feedfwd(x = data.matrix(grid[, c('x1', 'x2')]),
w1 = nnet30$w1,
w2 = nnet30$w2)
grid$class <- factor((ff_grid$output > .5) * 1,
labels = levels(spiral$class))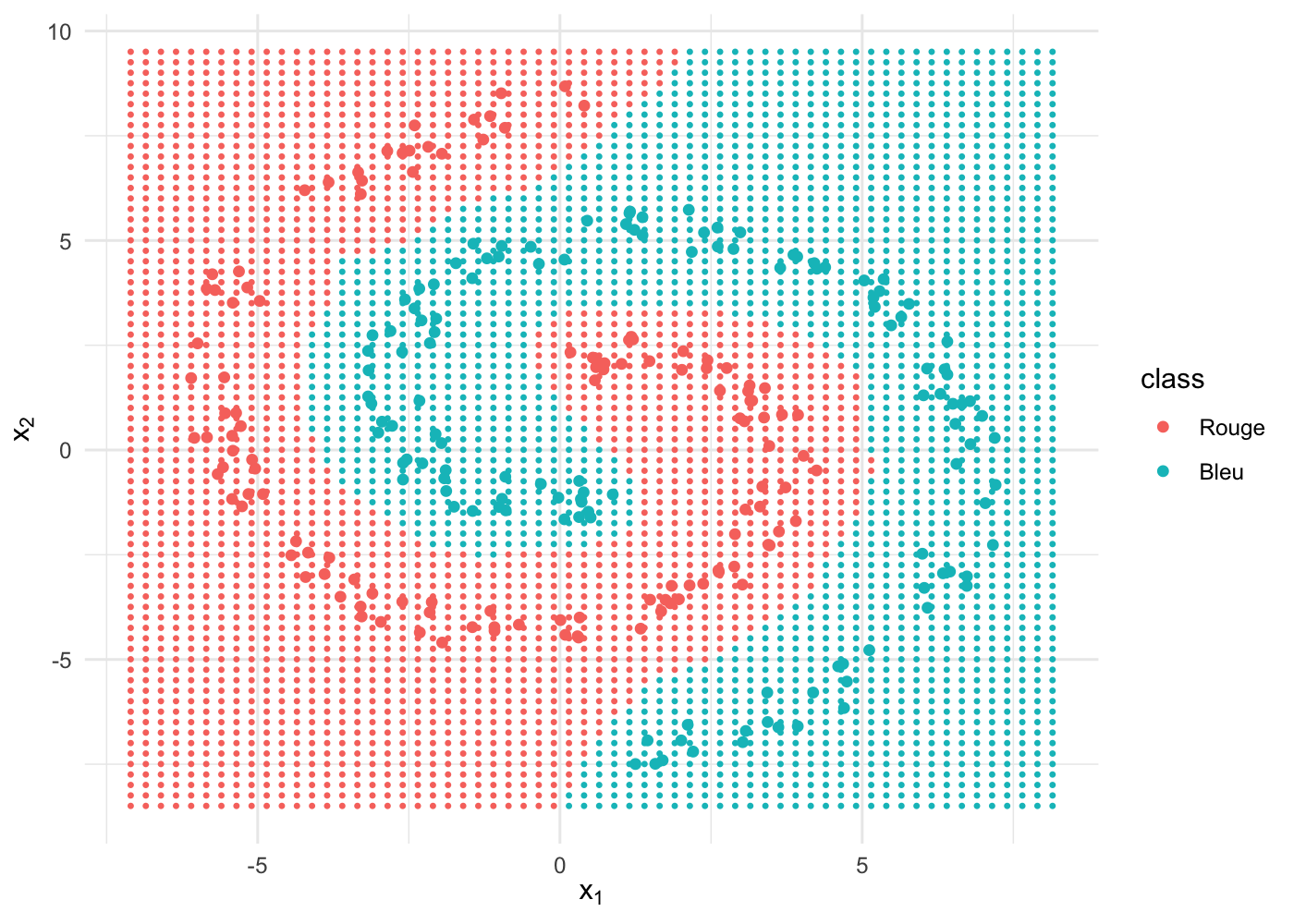
La frontière de décision est totalement arrondie, parfaitement adaptée à nos données. La performance est de … 100% !!!
Testons à présent le cas avec un seul neurone dans la couche cachée :
nnet1 <- train(x, y, hidden = 1, iterations = 1e5)Nous voilà de retour au cas de la régression linéaire, une frontière de décision linéaire et une performance médiocre :
ff_grid <- feedfwd(x = data.matrix(grid[, c('x1', 'x2')]),
w1 = nnet1$w1,
w2 = nnet1$w2)
grid$class <- factor((ff_grid$output > .5) * 1,
labels = levels(spiral$class))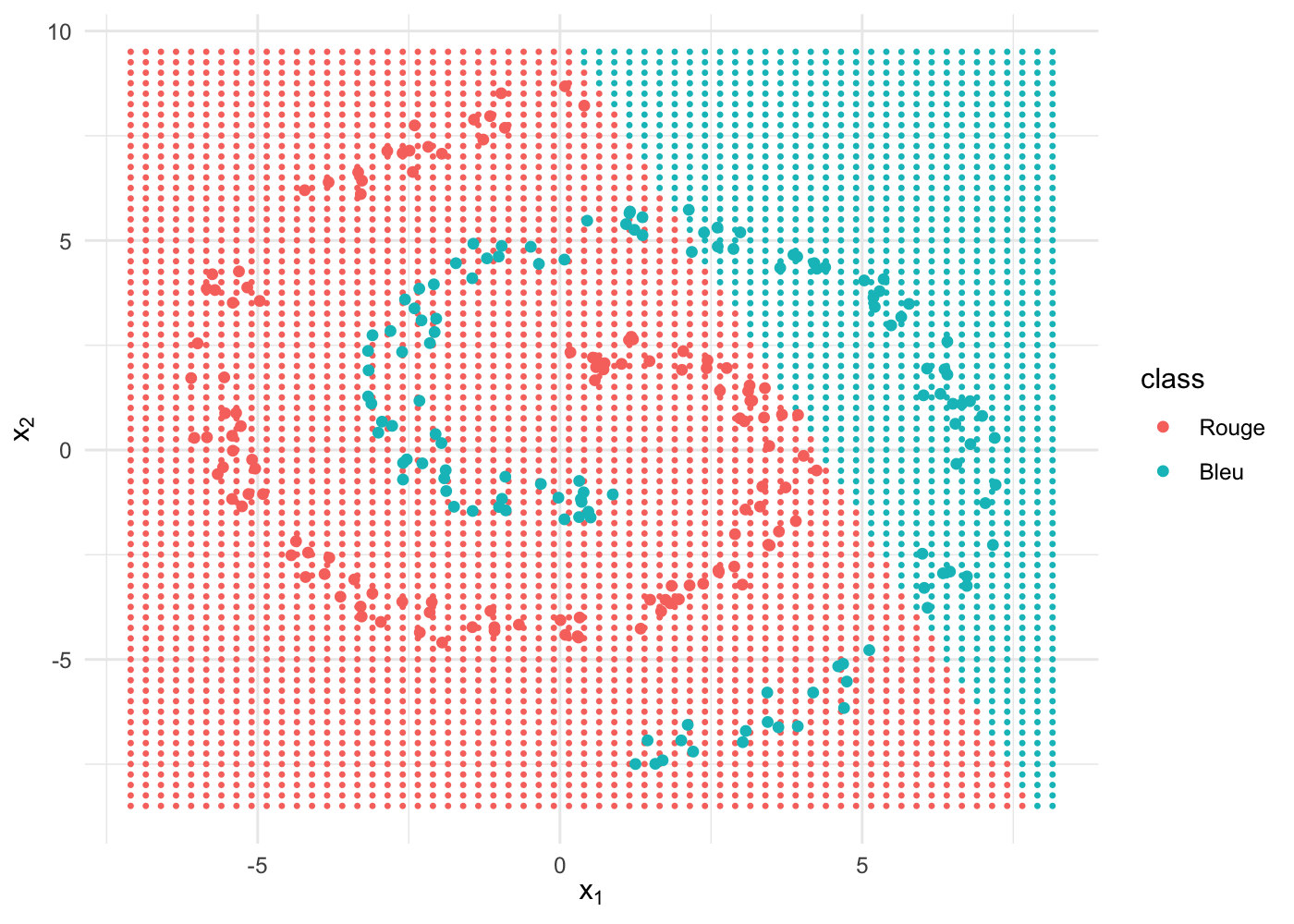
Conclusion :
Les réseaux de neurones sont une classe d’algorithmes d’apprentissage automatique capables de résoudre une large palette de problèmes complexes. Malgré une réputation de boîte noire, un réseau de neurones est à peu de choses près un ensemble de fonctions inter-connectées. C’est justement de cette collaboration entre fonctions simples, agrémentées d’une pincée de non-linéarité (notamment grâce aux fonctions d’activation) que naît la puissance d’apprentissage des réseaux de neurones.
Il existe des architectures de réseaux plus complexes que celle que nous avons vue, capables de tâches très avancées comme la synthèse vocale ou la traduction de texte, et qui sont déjà employés dans énormément d’applications de notre quotidien. En voici un aperçu non exhaustif.
Bien sûr, le Deep Learning “moderne” utilise des librairies logicielles spécialisées très efficaces comme PyTorch ou TensorFlow.
Côté hardware, vu le caractère hautement itératif et le grand besoin en puissance de calcul, on utilise très souvent des processeurs graphiques ou GPU (les mêmes que ceux employés pour faire tourner des jeux vidéos ou miner des cryptomonnaies en PoW) plutôt que le micro-processeur de son laptop. On obtient ainsi une grande accélération de l’entraînement des modèles.
Un super article sur les avancées récentes (fin 2017 mais toujours pertinent!) est par ici !
Pour aller plus loin, je conseille vivement de suivre le cours mis en ligne par l’équipe d’Andrew Ng sur Coursera et qui s’appelle Neural Networks and Deep Learning. Il est particulièrement adapté aux débutants car il part véritablement de zéro.
Sinon, pour attaquer le sujet sérieusement avec R ou Python sans trop se prendre la tête, Keras est la meilleure solution du moment et permet d’aller très très vite.
Sources :
- Google Playground
- Building a neural network from scratch in R par David Selby
- Implementing a Neural Network from Scratch in Python – An Introduction
N’hésitez pas à me transmettre vos remarques, ceci est une première version largement améliorable et sûrement incomplète
Merci ! 😉
- Merci pour votre lecture ! 😊👋
Anas EL KHALOUI
